Hash Tables

Note

Objectives

1. Explain and trace hash table algorithms such as insertion and search.
2. Evaluate how a hash table will behave in response to a given data type.
3. Analyze the runtime of a hash table with a given bucket data structure.

Code: SeparateChainingHashST.java

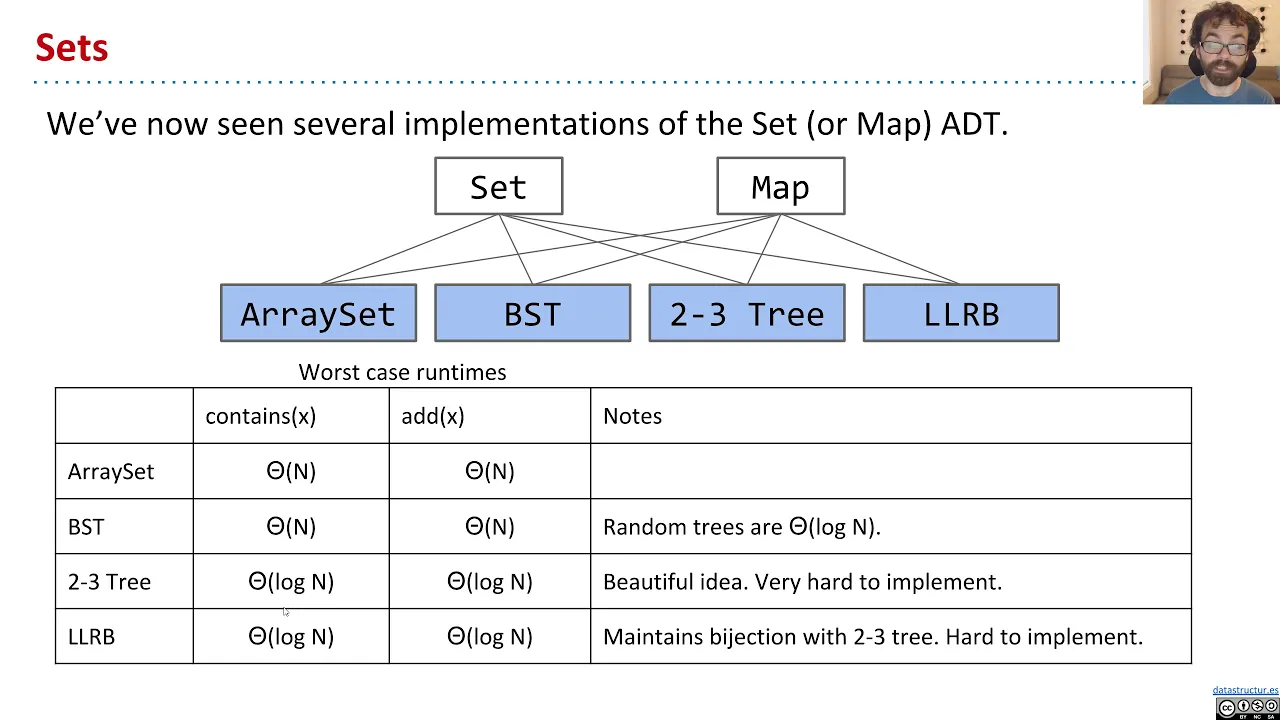
Java's TreeSet and TreeMap classes are implemented using red-black trees that guarantee logarithmic time for most individual element operations. This is a massive improvement over sequential search: a balanced search tree containing over 1 million elements has a height on the order of about 20!

But it turns out that we can do even better by studying Java's HashSet and HashMap classes, which are implemented using hash tables. Under certain conditions, hash tables can have constant time for most individual element operations—regardless of whether your hash table contains 1 million, 1 billion, 1 trillion, or even more elements.

Data-indexed sets

Unlike linked lists, indexing into any position in an array is a constant time operation. DataIndexedIntegerSet uses this idea of an array to implement a set of integers. It maintains a boolean[] present of length 2 billion, one index for almost every non-negative integer. The boolean value stored at each index present[x] represents whether or not the integer x is in the set. Watch the complete video.

While this implementation is simple and fast, it takes a lot of memory to store the 2-billion length present array—and it doesn't even work with negative integers or other data types. How might we generalize this concept to support strings?

A DataIndexedStringSet could have a 27-element array: 1 array index for each lowercase letter in the English alphabet starting at index 1. A word starting with the letter 'a' goes to index 1, 'b' goes to index 2, 'c' goes to index 3, etc. To study the behavior of this program, let's consider these three test cases.

1. DataIndexedStringSet set = new DataIndexedStringSet();
   set.add("cat");
   
   System.out.println(set.contains("car"));

2. DataIndexedStringSet set = new DataIndexedStringSet();
   set.add("cat");
   
   set.add("car");
   set.remove("cat");
   System.out.println(set.contains("car"));

3. DataIndexedStringSet set = new DataIndexedStringSet();
   set.add("cat");
   
   set.add("dog");
   System.out.println(set.contains("dog"));

Some of these test cases work as we would expect a set to work, but other test cases don't work.

Which of these test cases will behave correctly?

Only the third test case works as expected. In the other two test cases, "cat" and "car" collide because they share the same index, so changes to "cat" will also affect "car" and vice versa. This is unexpected because the set should treat the two strings as different from each other, but it turns out that changing the state of one will also change the state of the other.

Collisions

A collision occurs when two or more elements share the same index. One way we can avoid collisions in a DataIndexedStringSet is to be more careful about how we assign each English word. If we make sure every English word has its own unique index, then we can avoid collisions!

Suppose the string "a" goes to 1, "b" goes to 2, "c" goes to 3, ..., and "z" goes to 26. Then the string "aa" should go to 27, "ab" to 28, "ac" to 29, and so forth. Since there are 26 letters in the English alphabet, we call this enumeration scheme base 26. Each string gets its own number, so as strings get longer and longer, the number assigned to each string grows larger and larger as well. We can compute the index for "cat" as $(3 \cdot 26^2) + (1 \cdot 26^1) + (20 \cdot 26^0) = 2074$ since "c" has value 3, "a" has value 1, and "t" has value 20 and the powers of 26 help us avoid collisions with any other options in the subsequent letters.

So long as we pick a base that's at least 26, this hash function is guaranteed to assign each lowercase English word a unique integer. But it doesn't work with uppercase characters or punctuation. Furthermore, if we want to support other languages than English, we'll need an even larger base. For example, there are 40,959 characters in the Chinese language alone. If we wanted to support all the possible characters in the Java built-in char type—which includes emojis, punctuation, and characters across many languages—we would need base 65536. Hash values generated this way will grow exponentially with respect to the length of the string!

Separate chaining hash tables

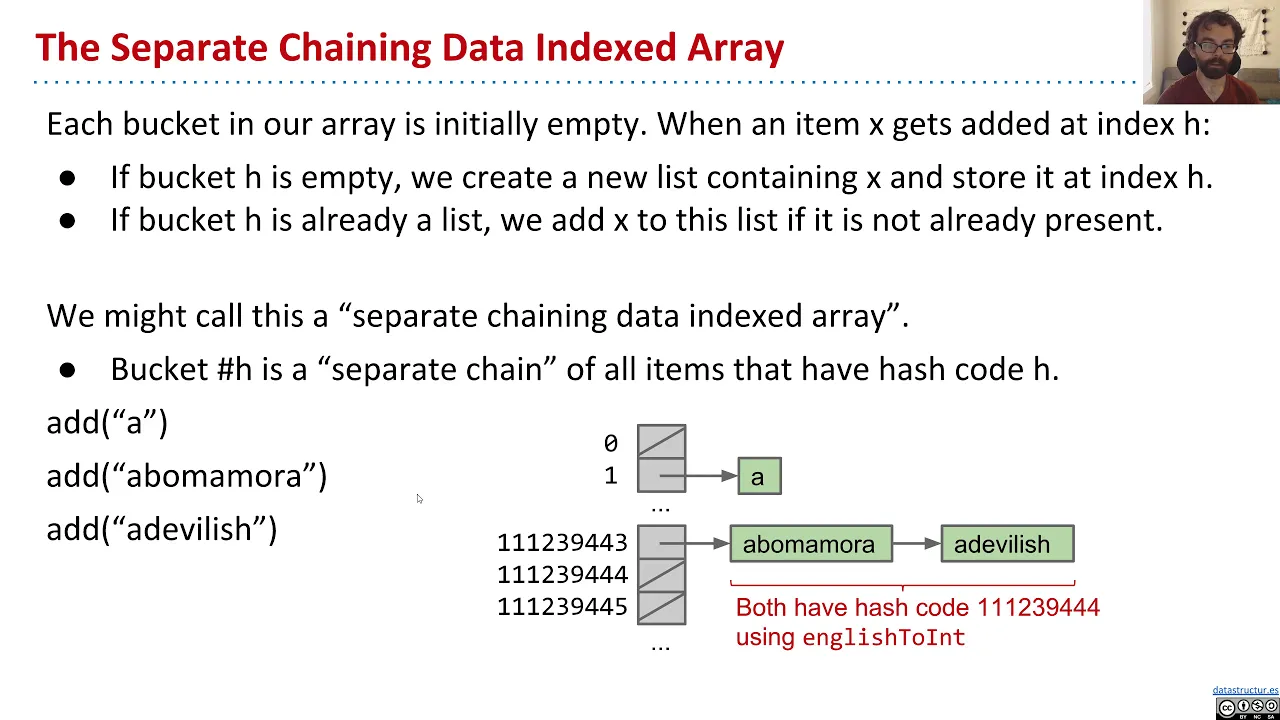
In practice, collisions are unavoidable. Instead of trying to avoid collisions by assigning a unique number to each element, separate chaining hash tables handle collisions by replacing the boolean[] present with an array of buckets, where each bucket can store zero or more elements. Watch the following two videos.

Since separate chaining addresses collisions, we can now use smaller arrays. Instead of directly using the hash code as the index into the array, take the modulus of the hash code to compute an index into the array.

Separate chaining turns the process from a single step to multiple steps:

1. Call the hash function on the given element to get a hash code, aka the number for that element.
2. Compute the bucket index by taking the modulus of the hash code by the array length.
3. Search the bucket for the given element.

Important

Review the Hash Tables slides to see how these steps come together.

Separate chaining comes with a cost. The worst case runtime for adding, removing, or finding an item is now in $\Theta(Q)$ where $Q$ is the size of the largest bucket.

In general, the runtime of a separate chaining hash table is determined by a number of factors. We'll often need to ask a couple of questions about the hash function and the hash table before we can properly analyze or predict the data structure performance.

• What is the hash function's likelihood of collisions?
• What is the strategy for resizing the hash table.
• What is the runtime for searching the bucket data structure.