Graph Traversals

Note

Objectives

1. Trace and explain each data structure in BFS and DFS graph traversal.
2. Analyze the runtime of a graph algorithm in terms of vertices and edges.
3. Define an appropriate graph abstraction for a given image processing problem.

Code: BreadthFirstPaths.java, DepthFirstPaths.java

Cool: Nonverbal instructions for Graph Scan

How do we use a graph to solve problems like computing navigation directions? We need a way to traverse a graph or explore all of its data. To traverse a tree, we can start from the overall root and recursively work our way down. To traverse a hash table, we can start from bucket index 0 and iterate over all the separate chains. But where do we start a graph traversal? Watch the complete video.

By applying the idea of recursive tree traversal, we discovered a graph algorithm called depth-first search (DFS): a recursive graph traversal algorithm that explores as far as possible from a given start vertex until it reaches a base case and needs to backtrack.

void dfs(Graph<V> graph, V start) {
    dfs(graph, start, new HashSet<>());
}

dfs(Graph<V> graph, V from, Set<V> visited) {
    // Process the current vertex by printing it out
    System.out.println(from);
    visited.add(from);

    for (Edge<V> edge : graph.neighbors(from)) {
        V to = edge.to;
        if (!visited.contains(to)) {
            dfs(graph, to, visited);
        }
    }
}

Depth-first search is often compared to another graph traversal algorithm called breadth-first search (BFS): an iterative graph traversal algorithm that expands outward, level-by-level, from a given start vertex. BFS will be the template for many of the graph algorithms that we'll learn in the coming lessons. Watch the following video through the 9:53 mark.

void bfs(Graph<V> graph, V start) {
    Queue<V> perimeter = new ArrayDeque<>();
    Set<V> visited = new HashSet<>();

    perimeter.add(start);
    visited.add(start);

    while (!perimeter.isEmpty()) {
        V from = perimeter.remove();
        // Process the current vertex by printing it out
        System.out.println(from);

        for (Edge<V> edge : graph.neighbors(from)) {
            V to = edge.to;
            if (!visited.contains(to)) {
                perimeter.add(to);
                visited.add(to);
            }
        }
    }
}

BFS and DFS represent two ways of traversing over all the data in a graph by visiting all the vertices and checking all the edges. BFS and DFS are like the for loops of graphs: on their own, they don't solve a specific problem, but they are an important building block for graph algorithms. Watch the following video through the 10:53 mark.

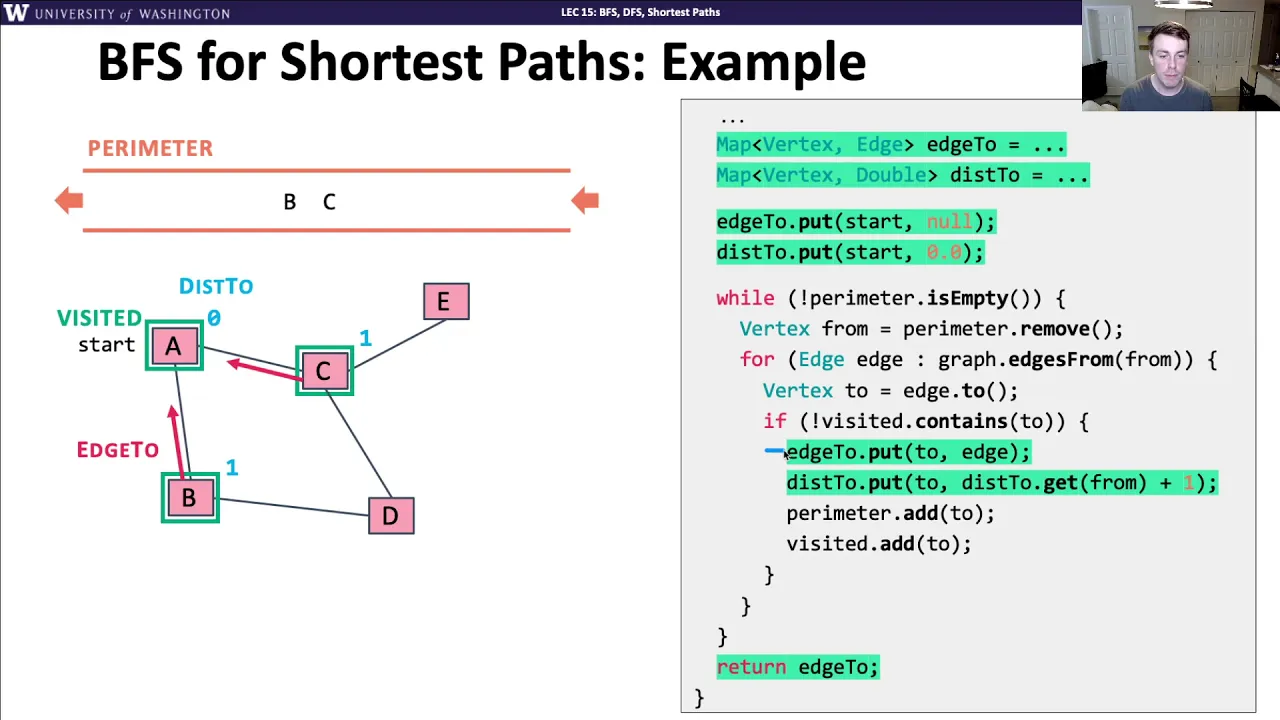
BFS provides a lot more utility than DFS in this context because it can be used to find the shortest paths in a unweighted graph with the help of two extra data structures called edgeTo and distTo.

• Map<V, Edge<V>> edgeTo maps each vertex to the edge used to reach it in the BFS traversal.
• Map<V, Integer> distTo maps each vertex to the number of edges from the start vertex.