Binary Heaps

Note

Objectives

1. Apply sink/swim operations to trace heap element insertion and removal.
2. Identify possible binary heap indices for the n-th smallest value.
3. Given an array index, find the parent, left child, and right child indexes.

Code: MinPQ.java

Compared to binary search trees, 2-3 trees and left-leaning red-black trees provided two solutions to avoiding worst case height. But neither a 2-3 tree nor a left-leaning red-black tree maintain a perfectly-balanced binary search tree. A 2-3 tree maintains perfect balance, but needs 3-child nodes. A left-leaning red-black tree is a binary search tree, but it doesn't maintain perfect balance: in the worst case, the left side can be up to double the height of the right side.

How do we even define perfect balance? One definition is completeness: a complete tree is a tree where every level, except possibly the last level, is completely filled; if the last level is not completely filled, all nodes must be as far left as possible. It's not easy maintaining a complete binary search tree: a tree that simultaneously satisfies all three of the definitions for complete tree, binary tree, and search tree. Of the tree data structures that we've studied, our best approaches only satisfy two out of three properties:

• A 2–3 tree satisfies the definitions for complete tree and search tree but not binary tree.
• A LLRB tree satisfies the definitions for binary tree and search tree but not complete tree.
• A binary heap satisfies the definitions for complete tree and binary tree but not search tree.

What can we do with a binary tree without the search tree property? 2-3 trees and LLRB trees provided efficient implementations for sets and maps because of the combination of their search tree property and height invariants. Binary heaps instead implement a different abstract data type called priority queue.

Priority queues

A priority queue is collection of elements organized according to their associated priority values. Just as a map has keys and corresponding values, a priority queues has elements and corresponding priorities. A min-oriented priority queue or MinPQ allows us to add an element with a corresponding priority value and also peek or remove an element with the minimum priority value. Likewise, the max-oriented priority queue or MaxPQ could be defined with methods enabling access to an element with the maximum priority value.

Priority queues often have direct real-world applications. For example, they can be used to triage patients in a hospital emergency room. Rather than serving patients first-come, first-served (as in a regular queue), a priority queue can be used to ensure patients with the most severe or time-sensitive conditions are treated first even if someone else arrived earlier. Priority queues differ from sets in two ways.

1. Multiple elements can share the same priority value. For example, two patients can be equally in need of care. Ties between priority value can go either way because either one is an element with the minimum (or maximum) priority value.
2. In some implementations, duplicate elements are allowed. This doesn't make sense for the emergency room application since you can't have two copies of a person, but we'll later see some algorithms that rely on storing duplicates.

Heap invariant

To implement a priority queue, binary heaps maintain a heap invariant that depends on whether the heap implements a MinPQ or a MaxPQ.

• For a MinPQ, the min-heap invariant requires that the priority of an element must be less than or equal to the priority of all its children.
• For a MaxPQ, the max-heap invariant requires that the priority of an element must be greater than or equal to the priority of all its children.

Important

For simplicity, our visualizations will only show the priority value. In practice, we'll often want to have elements that are different from their priority values.

Review the slides on how to Binary Min-Heap Operations.

Implementing peekMin just requires returning the overall root element because the min-heap invariant ensures that the element with the minimum priority value will be stored at the very top of the tree. Implementing removeMin, however, requires more work to maintain the completeness property.

1. Swap the root with the last leaf.
2. Remove the last leaf.
3. Sink the new root to its proper place, promoting the lower-priority child.

The sink (percolate down) private helper method repeatedly swaps the current node with the lower-priority child until heap invariants are restored. Likewise, we can define a swim private helper method to repeatedly swap the current node with its parent until heap invariants are restored. The public add method can be implemented by adding the element to the next open leaf position before swimming the element to restore heap invariants.

Array representation

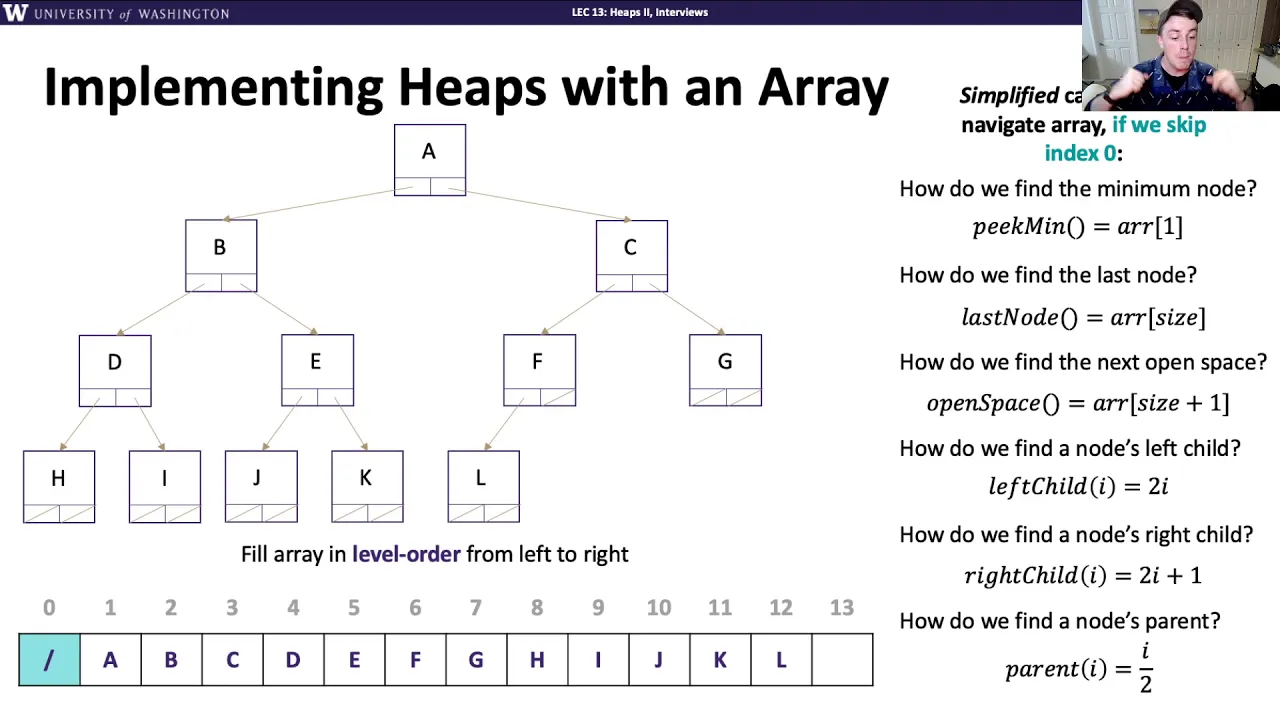
In practice, the main advantage of using a binary heap to implement a priority queue is due to a way that we can represent the tree using an array for improved memory locality and better caching effects. In practice, binary heaps are always represented as arrays—it's the default that other programmers will assume when talking about binary heaps. Watch the following video through the 6:46 mark.

The node representation that we've been discussing so far explicitly maintains tree structure through a hierarchy of parent-to-child references. The new array representation implicitly maintains tree structure through a mapping between array indices and tree location so that we can move up (to the parents) and down (to the children) using integer arithmetic.

Important

Review the Binary Heap Demo which shows how a binary max-heap changes in response to adding or removing elements.

Then, open the VisuAlgo module on binary max-heaps. Press Esc to exit the e-Lecture Mode. Choose ExtractMax() from the bottom left menu and select 1x (Once) to see the result of removing the element associated with the maximum priority value. The red number under each node represents the index in the array representation of the tree.