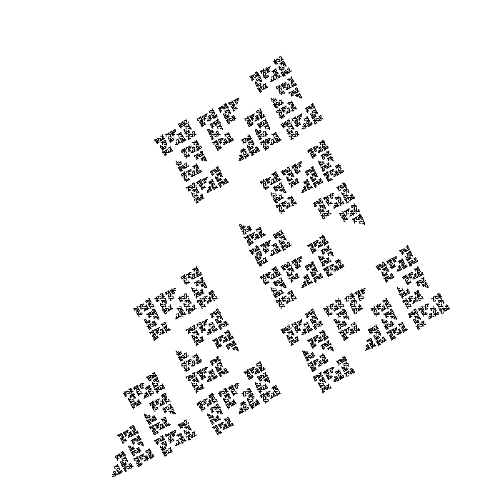An interactive GUI for creating neat fractal images.
Fractals, as they relate to this project, are cool mathematical figures that exhibit "self-similarity". This means that fractals are composed of smaller versions of themselves, or that there are many similar figures within a fractal. The purpose of this project was to create a versatile fractal "editor" that allows the user to create interesting fractals with the use of a few simple rules. The following explains the user interface and logic of the program.
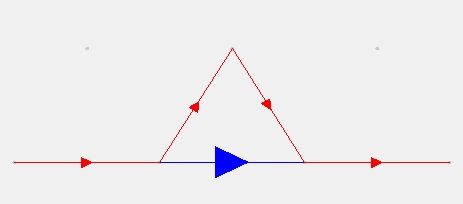
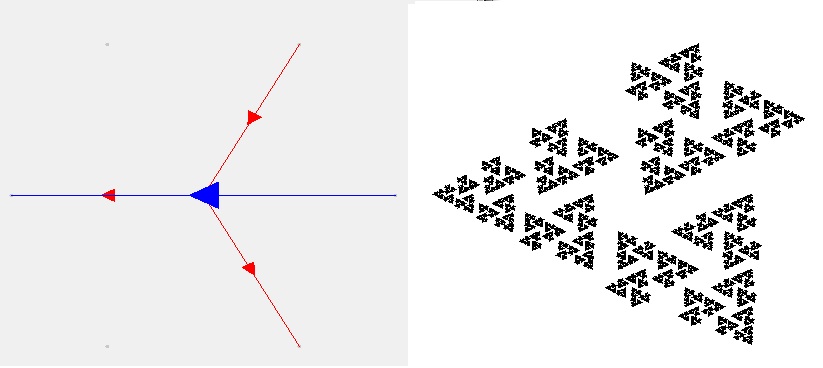
Any fractal created by this program is defined by a "generator". A generator consists of a set of vectors drawn in the x/y plane. For example:
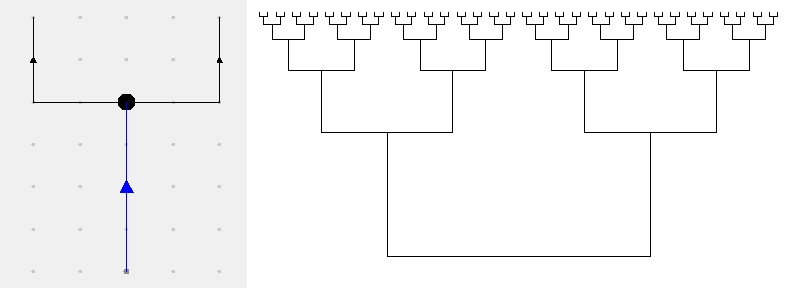
The blue arrow in the figure (covered by red vectors but extending from far left to far right) represents the reference vector. The red arrows in this figure represent recursive vectors. Fractals are generated in levels. A level-0 fractal consists simply of the generator vectors, excluding the reference vector. Now focus for a moment on the leftmost red recusive vector of our level-0 fractal, and consider overlaying a scaled copy of the generator onto this vector such that the reference vector in this copied generator aligns perfectly with our recursive vector. Now if we replace this leftmost recursive vector with the vectors of this scaled generator (excluding the reference vector), what we have essentially done is replaced the recursive vector from our level-0 fractal with a smaller level-0 fractal. This is the fundamental transformation used by this program to create fractals. By applying this transformation to each of the recursive vectors in the generator, we arrive at a level-1 instance of the fractal.
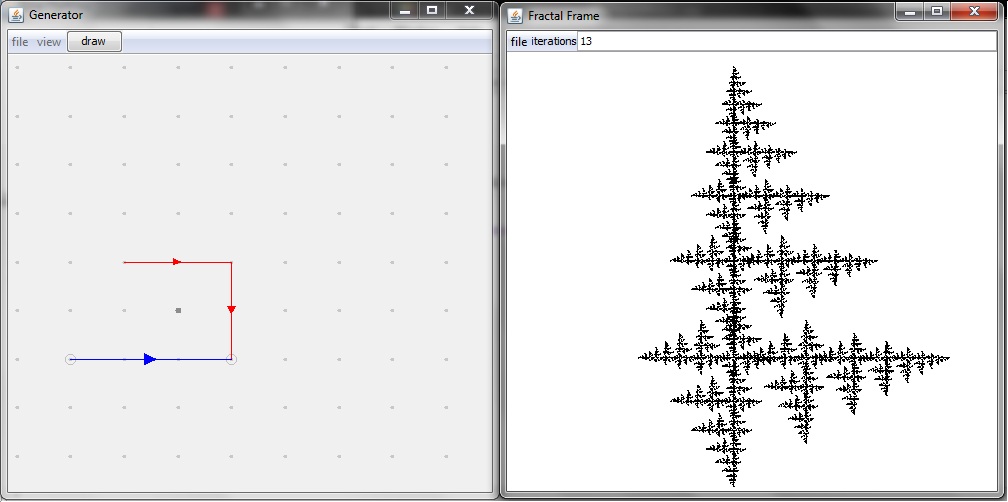
Notice that level-1 fractal consists entirely of recursive vectors, each a third the length of those in the level-0 fractal. We can iterate the transformation of the previous paragraph, replacing each recursive vector with a level-0 fractal (using the generator's reference vector for alignment), to achieve a level-2 fractal, and so on. Shown below is a level-5 version of this fractal.
The above fractal is a portion of a figure known as the Koch Snowflake. While the "true fractal" is actually level-N as N approaches infinity, this level-5 approximation is nearly indistinguishable to the eye from the true limiting figure.
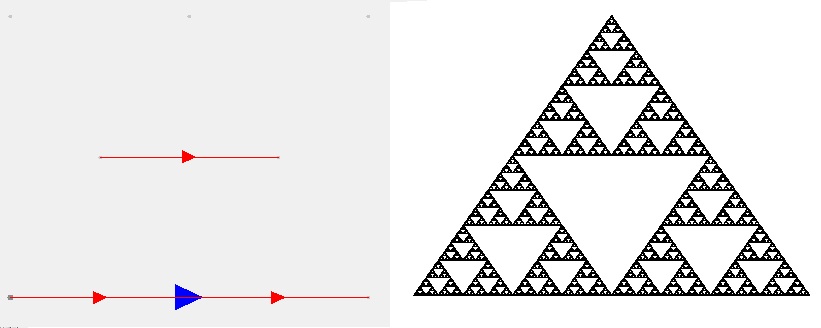
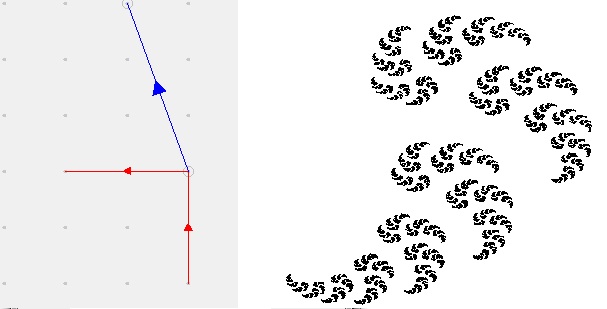
Here are some example fractals (some shown alongside their generators) that were generated with this software.