|
| 1 | + |
| 2 | +# 58. 区间和 |
| 3 | + |
| 4 | +[题目链接](https://kamacoder.com/problempage.php?pid=1070) |
| 5 | + |
| 6 | +题目描述 |
| 7 | + |
| 8 | +给定一个整数数组 Array,请计算该数组在每个指定区间内元素的总和。 |
| 9 | + |
| 10 | +输入描述 |
| 11 | + |
| 12 | +第一行输入为整数数组 Array 的长度 n,接下来 n 行,每行一个整数,表示数组的元素。随后的输入为需要计算总和的区间,直至文件结束。 |
| 13 | + |
| 14 | +输出描述 |
| 15 | + |
| 16 | +输出每个指定区间内元素的总和。 |
| 17 | + |
| 18 | +输入示例 |
| 19 | + |
| 20 | +``` |
| 21 | +5 |
| 22 | +1 |
| 23 | +2 |
| 24 | +3 |
| 25 | +4 |
| 26 | +5 |
| 27 | +0 1 |
| 28 | +1 3 |
| 29 | +``` |
| 30 | + |
| 31 | +输出示例 |
| 32 | + |
| 33 | +``` |
| 34 | +3 |
| 35 | +9 |
| 36 | +``` |
| 37 | + |
| 38 | +数据范围: |
| 39 | + |
| 40 | +0 < n <= 100000 |
| 41 | + |
| 42 | +## 思路 |
| 43 | + |
| 44 | +本题我们来讲解 数组 上常用的解题技巧:前缀和 |
| 45 | + |
| 46 | +首先来看本题,我们最直观的想法是什么? |
| 47 | + |
| 48 | +那就是给一个区间,然后 把这个区间的和都累加一遍不就得了,是一道简单不能再简单的题目。 |
| 49 | + |
| 50 | +代码如下: |
| 51 | + |
| 52 | +```CPP |
| 53 | +#include <iostream> |
| 54 | +#include <vector> |
| 55 | +using namespace std; |
| 56 | +int main() { |
| 57 | + int n, a, b; |
| 58 | + cin >> n; |
| 59 | + vector<int> vec(n); |
| 60 | + for (int i = 0; i < n; i++) cin >> vec[i]; |
| 61 | + while (cin >> a >> b) { |
| 62 | + int sum = 0; |
| 63 | + // 累加区间 a 到 b 的和 |
| 64 | + for (int i = a; i <= b; i++) sum += vec[i]; |
| 65 | + cout << sum << endl; |
| 66 | + } |
| 67 | +} |
| 68 | +``` |
| 69 | + |
| 70 | +代码一提交,发现超时了..... |
| 71 | + |
| 72 | +我在制作本题的时候,特别制作了大数据量查询,卡的就是这种暴力解法。 |
| 73 | + |
| 74 | +来举一个极端的例子,如果我查询m次,每次查询的范围都是从0 到 n - 1 |
| 75 | + |
| 76 | +那么该算法的时间复杂度是 O(n * m) m 是查询的次数 |
| 77 | + |
| 78 | +如果查询次数非常大的话,这个时间复杂度也是非常大的。 |
| 79 | + |
| 80 | +接下来我们来引入前缀和,看看前缀和如何解决这个问题。 |
| 81 | + |
| 82 | +前缀和的思想是重复利用计算过的子数组之和,从而降低区间查询需要累加计算的次数。 |
| 83 | + |
| 84 | +**前缀和 在涉及计算区间和的问题时非常有用**! |
| 85 | + |
| 86 | +前缀和的思路其实很简单,我给大家举个例子很容易就懂了。 |
| 87 | + |
| 88 | +例如,我们要统计 vec[i] 这个数组上的区间和。 |
| 89 | + |
| 90 | +我们先做累加,即 p[i] 表示 下标 0 到 i 的 vec[i] 累加 之和。 |
| 91 | + |
| 92 | +如图: |
| 93 | + |
| 94 | +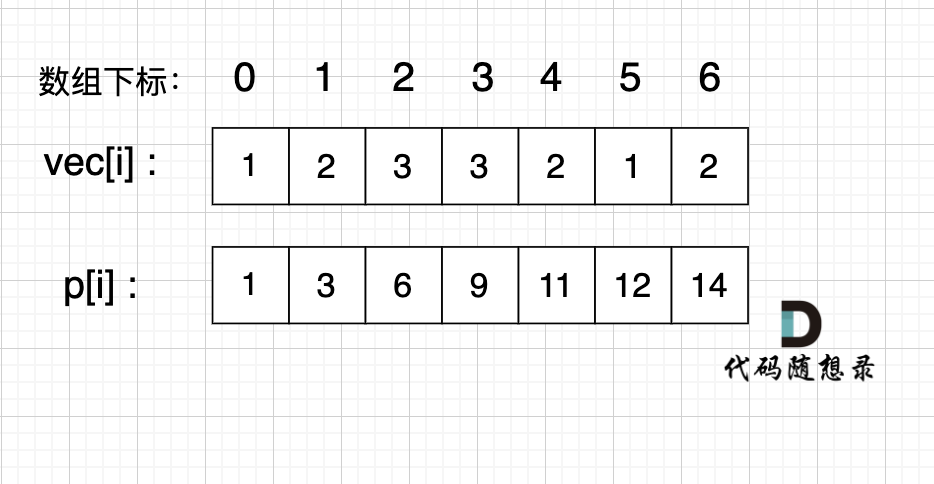 |
| 95 | + |
| 96 | + |
| 97 | +如果,我们想统计,在vec数组上 下标 2 到下标 5 之间的累加和,那是不是就用 p[5] - p[1] 就可以了。 |
| 98 | + |
| 99 | +为什么呢? |
| 100 | + |
| 101 | +p[1] = vec[0] + vec[1]; |
| 102 | + |
| 103 | +p[5] = vec[0] + vec[1] + vec[2] + vec[3] + vec[4] + vec[5]; |
| 104 | + |
| 105 | +p[5] - p[1] = vec[2] + vec[3] + vec[4] + vec[5]; |
| 106 | + |
| 107 | +这不就是我们要求的 下标 2 到下标 5 之间的累加和吗。 |
| 108 | + |
| 109 | +如图所示: |
| 110 | + |
| 111 | + |
| 112 | + |
| 113 | +p[5] - p[1] 就是 红色部分的区间和。 |
| 114 | + |
| 115 | +而 p 数组是我们之前就计算好的累加和,所以后面每次求区间和的之后 我们只需要 O(1)的操作。 |
| 116 | + |
| 117 | + |
| 118 | + |
| 119 | +```CPP |
| 120 | +#include <iostream> |
| 121 | +#include <vector> |
| 122 | +using namespace std; |
| 123 | +int main() { |
| 124 | + int n, a, b; |
| 125 | + cin >> n; |
| 126 | + vector<int> vec(n); |
| 127 | + vector<int> p(n); |
| 128 | + int presum = 0; |
| 129 | + for (int i = 0; i < n; i++) { |
| 130 | + cin >> vec[i]; |
| 131 | + presum += vec[i]; |
| 132 | + p[i] = presum; |
| 133 | + } |
| 134 | + |
| 135 | + while (cin >> a >> b) { |
| 136 | + int sum; |
| 137 | + if (a == 0) sum = p[b]; |
| 138 | + else sum = p[b] - p[a - 1]; |
| 139 | + cout << sum << endl; |
| 140 | + } |
| 141 | +} |
| 142 | + |
| 143 | +``` |
| 144 | + |
| 145 | +```CPP |
| 146 | +#include <iostream> |
| 147 | +#include <vector> |
| 148 | +using namespace std; |
| 149 | +int main() { |
| 150 | + int n, a, b; |
| 151 | + cin >> n; |
| 152 | + vector<int> vec(n); |
| 153 | + vector<int> p(n); |
| 154 | + int presum = 0; |
| 155 | + for (int i = 0; i < n; i++) { |
| 156 | + scanf("%d", &vec[i]); |
| 157 | + presum += vec[i]; |
| 158 | + p[i] = presum; |
| 159 | + } |
| 160 | + |
| 161 | + while (~scanf("%d%d", &a, &b)) { |
| 162 | + int sum; |
| 163 | + if (a == 0) sum = p[b]; |
| 164 | + else sum = p[b] - p[a - 1]; |
| 165 | + printf("%d\n", sum); |
| 166 | + } |
| 167 | +} |
| 168 | + |
| 169 | +``` |
| 170 | + |
| 171 | +```CPP |
| 172 | + |
| 173 | +#include<bits/stdc++.h> |
| 174 | +using namespace std; |
| 175 | + |
| 176 | + |
| 177 | +int main(){ |
| 178 | + int n, a, b; |
| 179 | + cin >> n; |
| 180 | + vector<int> vec(n + 1); |
| 181 | + vector<int> p(n + 1, 0); |
| 182 | + for(int i = 1; i <= n; i++) { |
| 183 | + scanf("%d", &vec[i]); |
| 184 | + p[i] = p[i - 1] + vec[i]; |
| 185 | + } |
| 186 | + while(~scanf("%d%d", &a, &b)){ |
| 187 | + printf("%d\n", p[b + 1] - p[a]); |
| 188 | + } |
| 189 | + return 0; |
| 190 | +} |
| 191 | +``` |
0 commit comments