diff --git a/src/main/java/g3501_3600/s3536_maximum_product_of_two_digits/Solution.java b/src/main/java/g3501_3600/s3536_maximum_product_of_two_digits/Solution.java
new file mode 100644
index 000000000..17d3a02b3
--- /dev/null
+++ b/src/main/java/g3501_3600/s3536_maximum_product_of_two_digits/Solution.java
@@ -0,0 +1,27 @@
+package g3501_3600.s3536_maximum_product_of_two_digits;
+
+// #Easy #Math #Sorting #2025_05_06_Time_1_ms_(95.82%)_Space_40.95_MB_(91.71%)
+
+public class Solution {
+ public int maxProduct(int n) {
+ int m1 = n % 10;
+ n /= 10;
+ int m2 = n % 10;
+ n /= 10;
+ while (n > 0) {
+ int a = n % 10;
+ if (a > m1) {
+ if (m1 > m2) {
+ m2 = m1;
+ }
+ m1 = a;
+ } else {
+ if (a > m2) {
+ m2 = a;
+ }
+ }
+ n /= 10;
+ }
+ return m1 * m2;
+ }
+}
diff --git a/src/main/java/g3501_3600/s3536_maximum_product_of_two_digits/readme.md b/src/main/java/g3501_3600/s3536_maximum_product_of_two_digits/readme.md
new file mode 100644
index 000000000..11f945253
--- /dev/null
+++ b/src/main/java/g3501_3600/s3536_maximum_product_of_two_digits/readme.md
@@ -0,0 +1,49 @@
+3536\. Maximum Product of Two Digits
+
+Easy
+
+You are given a positive integer `n`.
+
+Return the **maximum** product of any two digits in `n`.
+
+**Note:** You may use the **same** digit twice if it appears more than once in `n`.
+
+**Example 1:**
+
+**Input:** n = 31
+
+**Output:** 3
+
+**Explanation:**
+
+* The digits of `n` are `[3, 1]`.
+* The possible products of any two digits are: `3 * 1 = 3`.
+* The maximum product is 3.
+
+**Example 2:**
+
+**Input:** n = 22
+
+**Output:** 4
+
+**Explanation:**
+
+* The digits of `n` are `[2, 2]`.
+* The possible products of any two digits are: `2 * 2 = 4`.
+* The maximum product is 4.
+
+**Example 3:**
+
+**Input:** n = 124
+
+**Output:** 8
+
+**Explanation:**
+
+* The digits of `n` are `[1, 2, 4]`.
+* The possible products of any two digits are: `1 * 2 = 2`, `1 * 4 = 4`, `2 * 4 = 8`.
+* The maximum product is 8.
+
+**Constraints:**
+
+* 10 <= n <= 109
\ No newline at end of file
diff --git a/src/main/java/g3501_3600/s3537_fill_a_special_grid/Solution.java b/src/main/java/g3501_3600/s3537_fill_a_special_grid/Solution.java
new file mode 100644
index 000000000..cddb227ec
--- /dev/null
+++ b/src/main/java/g3501_3600/s3537_fill_a_special_grid/Solution.java
@@ -0,0 +1,32 @@
+package g3501_3600.s3537_fill_a_special_grid;
+
+// #Medium #Array #Matrix #Divide_and_Conquer
+// #2025_05_06_Time_2_ms_(100.00%)_Space_87.14_MB_(16.42%)
+
+public class Solution {
+ public int[][] specialGrid(int n) {
+ if (n == 0) {
+ return new int[][] {{0}};
+ }
+ int len = (int) Math.pow(2, n);
+ int[][] ans = new int[len][len];
+ int[] num = new int[] {(int) Math.pow(2, 2D * n) - 1};
+ backtrack(ans, len, len, 0, 0, num);
+ return ans;
+ }
+
+ private void backtrack(int[][] ans, int m, int n, int x, int y, int[] num) {
+ if (m == 2 && n == 2) {
+ ans[x][y] = num[0];
+ ans[x + 1][y] = num[0] - 1;
+ ans[x + 1][y + 1] = num[0] - 2;
+ ans[x][y + 1] = num[0] - 3;
+ num[0] -= 4;
+ return;
+ }
+ backtrack(ans, m / 2, n / 2, x, y, num);
+ backtrack(ans, m / 2, n / 2, x + m / 2, y, num);
+ backtrack(ans, m / 2, n / 2, x + m / 2, y + n / 2, num);
+ backtrack(ans, m / 2, n / 2, x, y + n / 2, num);
+ }
+}
diff --git a/src/main/java/g3501_3600/s3537_fill_a_special_grid/readme.md b/src/main/java/g3501_3600/s3537_fill_a_special_grid/readme.md
new file mode 100644
index 000000000..e0ee432a9
--- /dev/null
+++ b/src/main/java/g3501_3600/s3537_fill_a_special_grid/readme.md
@@ -0,0 +1,67 @@
+3537\. Fill a Special Grid
+
+Medium
+
+You are given a non-negative integer `n` representing a 2n x 2n grid. You must fill the grid with integers from 0 to 22n - 1 to make it **special**. A grid is **special** if it satisfies **all** the following conditions:
+
+* All numbers in the top-right quadrant are smaller than those in the bottom-right quadrant.
+* All numbers in the bottom-right quadrant are smaller than those in the bottom-left quadrant.
+* All numbers in the bottom-left quadrant are smaller than those in the top-left quadrant.
+* Each of its quadrants is also a special grid.
+
+Return the **special** 2n x 2n grid.
+
+**Note**: Any 1x1 grid is special.
+
+**Example 1:**
+
+**Input:** n = 0
+
+**Output:** [[0]]
+
+**Explanation:**
+
+The only number that can be placed is 0, and there is only one possible position in the grid.
+
+**Example 2:**
+
+**Input:** n = 1
+
+**Output:** [[3,0],[2,1]]
+
+**Explanation:**
+
+The numbers in each quadrant are:
+
+* Top-right: 0
+* Bottom-right: 1
+* Bottom-left: 2
+* Top-left: 3
+
+Since `0 < 1 < 2 < 3`, this satisfies the given constraints.
+
+**Example 3:**
+
+**Input:** n = 2
+
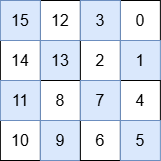
+**Output:** [[15,12,3,0],[14,13,2,1],[11,8,7,4],[10,9,6,5]]
+
+**Explanation:**
+
+
+
+The numbers in each quadrant are:
+
+* Top-right: 3, 0, 2, 1
+* Bottom-right: 7, 4, 6, 5
+* Bottom-left: 11, 8, 10, 9
+* Top-left: 15, 12, 14, 13
+* `max(3, 0, 2, 1) < min(7, 4, 6, 5)`
+* `max(7, 4, 6, 5) < min(11, 8, 10, 9)`
+* `max(11, 8, 10, 9) < min(15, 12, 14, 13)`
+
+This satisfies the first three requirements. Additionally, each quadrant is also a special grid. Thus, this is a special grid.
+
+**Constraints:**
+
+* `0 <= n <= 10`
\ No newline at end of file
diff --git a/src/main/java/g3501_3600/s3538_merge_operations_for_minimum_travel_time/Solution.java b/src/main/java/g3501_3600/s3538_merge_operations_for_minimum_travel_time/Solution.java
new file mode 100644
index 000000000..202bd32f6
--- /dev/null
+++ b/src/main/java/g3501_3600/s3538_merge_operations_for_minimum_travel_time/Solution.java
@@ -0,0 +1,43 @@
+package g3501_3600.s3538_merge_operations_for_minimum_travel_time;
+
+// #Hard #Array #Dynamic_Programming #Prefix_Sum
+// #2025_05_06_Time_7_ms_(99.32%)_Space_45.14_MB_(87.16%)
+
+@SuppressWarnings({"unused", "java:S1172"})
+public class Solution {
+ public int minTravelTime(int l, int n, int k, int[] position, int[] time) {
+ int[][][] dp = new int[n][k + 1][k + 1];
+ for (int i = 0; i < n; i++) {
+ for (int j = 0; j <= k; j++) {
+ for (int m = 0; m <= k; m++) {
+ dp[i][j][m] = Integer.MAX_VALUE;
+ }
+ }
+ }
+ dp[0][0][0] = 0;
+ for (int i = 0; i < n - 1; i++) {
+ int currTime = 0;
+ for (int curr = 0; curr <= k && curr <= i; curr++) {
+ currTime += time[i - curr];
+ for (int used = 0; used <= k; used++) {
+ if (dp[i][curr][used] == Integer.MAX_VALUE) {
+ continue;
+ }
+ for (int next = 0; next <= k - used && next <= n - i - 2; next++) {
+ int nextI = i + next + 1;
+ dp[nextI][next][next + used] =
+ Math.min(
+ dp[nextI][next][next + used],
+ dp[i][curr][used]
+ + (position[nextI] - position[i]) * currTime);
+ }
+ }
+ }
+ }
+ int ans = Integer.MAX_VALUE;
+ for (int curr = 0; curr <= k; curr++) {
+ ans = Math.min(ans, dp[n - 1][curr][k]);
+ }
+ return ans;
+ }
+}
diff --git a/src/main/java/g3501_3600/s3538_merge_operations_for_minimum_travel_time/readme.md b/src/main/java/g3501_3600/s3538_merge_operations_for_minimum_travel_time/readme.md
new file mode 100644
index 000000000..047bffd70
--- /dev/null
+++ b/src/main/java/g3501_3600/s3538_merge_operations_for_minimum_travel_time/readme.md
@@ -0,0 +1,71 @@
+3538\. Merge Operations for Minimum Travel Time
+
+Hard
+
+You are given a straight road of length `l` km, an integer `n`, an integer `k`**,** and **two** integer arrays, `position` and `time`, each of length `n`.
+
+The array `position` lists the positions (in km) of signs in **strictly** increasing order (with `position[0] = 0` and `position[n - 1] = l`).
+
+Each `time[i]` represents the time (in minutes) required to travel 1 km between `position[i]` and `position[i + 1]`.
+
+You **must** perform **exactly** `k` merge operations. In one merge, you can choose any **two** adjacent signs at indices `i` and `i + 1` (with `i > 0` and `i + 1 < n`) and:
+
+* Update the sign at index `i + 1` so that its time becomes `time[i] + time[i + 1]`.
+* Remove the sign at index `i`.
+
+Return the **minimum** **total** **travel time** (in minutes) to travel from 0 to `l` after **exactly** `k` merges.
+
+**Example 1:**
+
+**Input:** l = 10, n = 4, k = 1, position = [0,3,8,10], time = [5,8,3,6]
+
+**Output:** 62
+
+**Explanation:**
+
+* Merge the signs at indices 1 and 2. Remove the sign at index 1, and change the time at index 2 to `8 + 3 = 11`.
+
+* After the merge:
+ * `position` array: `[0, 8, 10]`
+ * `time` array: `[5, 11, 6]`
+
+| Segment | Distance (km) | Time per km (min) | Segment Travel Time (min) |
+|-----------|---------------|-------------------|----------------------------|
+| 0 → 8 | 8 | 5 | 8 × 5 = 40 |
+| 8 → 10 | 2 | 11 | 2 × 11 = 22 |
+
+
+* Total Travel Time: `40 + 22 = 62`, which is the minimum possible time after exactly 1 merge.
+
+**Example 2:**
+
+**Input:** l = 5, n = 5, k = 1, position = [0,1,2,3,5], time = [8,3,9,3,3]
+
+**Output:** 34
+
+**Explanation:**
+
+* Merge the signs at indices 1 and 2. Remove the sign at index 1, and change the time at index 2 to `3 + 9 = 12`.
+* After the merge:
+ * `position` array: `[0, 2, 3, 5]`
+ * `time` array: `[8, 12, 3, 3]`
+
+| Segment | Distance (km) | Time per km (min) | Segment Travel Time (min) |
+|-----------|---------------|-------------------|----------------------------|
+| 0 → 2 | 2 | 8 | 2 × 8 = 16 |
+| 2 → 3 | 1 | 12 | 1 × 12 = 12 |
+| 3 → 5 | 2 | 3 | 2 × 3 = 6 |
+
+* Total Travel Time: `16 + 12 + 6 = 34`**,** which is the minimum possible time after exactly 1 merge.
+
+**Constraints:**
+
+* 1 <= l <= 105
+* `2 <= n <= min(l + 1, 50)`
+* `0 <= k <= min(n - 2, 10)`
+* `position.length == n`
+* `position[0] = 0` and `position[n - 1] = l`
+* `position` is sorted in strictly increasing order.
+* `time.length == n`
+* `1 <= time[i] <= 100`
+* `1 <= sum(time) <= 100`
\ No newline at end of file
diff --git a/src/main/java/g3501_3600/s3539_find_sum_of_array_product_of_magical_sequences/Solution.java b/src/main/java/g3501_3600/s3539_find_sum_of_array_product_of_magical_sequences/Solution.java
new file mode 100644
index 000000000..5d65ff0ec
--- /dev/null
+++ b/src/main/java/g3501_3600/s3539_find_sum_of_array_product_of_magical_sequences/Solution.java
@@ -0,0 +1,87 @@
+package g3501_3600.s3539_find_sum_of_array_product_of_magical_sequences;
+
+// #Hard #Array #Dynamic_Programming #Math #Bit_Manipulation #Bitmask #Combinatorics
+// #2025_05_06_Time_39_ms_(95.71%)_Space_44.58_MB_(98.57%)
+
+import java.util.Arrays;
+
+public class Solution {
+ private static final int MOD = 1_000_000_007;
+ private static final int[][] C = precomputeBinom(31);
+ private static final int[] P = precomputePop(31);
+
+ public int magicalSum(int m, int k, int[] nums) {
+ int n = nums.length;
+ long[][] pow = new long[n][m + 1];
+ for (int j = 0; j < n; j++) {
+ pow[j][0] = 1L;
+ for (int c = 1; c <= m; c++) {
+ pow[j][c] = pow[j][c - 1] * nums[j] % MOD;
+ }
+ }
+ long[][][] dp = new long[m + 1][k + 1][m + 1];
+ long[][][] next = new long[m + 1][k + 1][m + 1];
+ dp[0][0][0] = 1L;
+ for (int i = 0; i < n; i++) {
+ for (int t = 0; t <= m; t++) {
+ for (int o = 0; o <= k; o++) {
+ Arrays.fill(next[t][o], 0L);
+ }
+ }
+ for (int t = 0; t <= m; t++) {
+ for (int o = 0; o <= k; o++) {
+ for (int c = 0; c <= m; c++) {
+ if (dp[t][o][c] == 0) {
+ continue;
+ }
+ for (int cc = 0; cc <= m - t; cc++) {
+ int total = c + cc;
+ if (o + (total & 1) > k) {
+ continue;
+ }
+ next[t + cc][o + (total & 1)][total >>> 1] =
+ (next[t + cc][o + (total & 1)][total >>> 1]
+ + dp[t][o][c]
+ * C[m - t][cc]
+ % MOD
+ * pow[i][cc]
+ % MOD)
+ % MOD;
+ }
+ }
+ }
+ }
+ long[][][] tmp = dp;
+ dp = next;
+ next = tmp;
+ }
+ long res = 0;
+ for (int o = 0; o <= k; o++) {
+ for (int c = 0; c <= m; c++) {
+ if (o + P[c] == k) {
+ res = (res + dp[m][o][c]) % MOD;
+ }
+ }
+ }
+ return (int) res;
+ }
+
+ private static int[][] precomputeBinom(int max) {
+ int[][] res = new int[max][max];
+ for (int i = 0; i < max; i++) {
+ res[i][0] = res[i][i] = 1;
+ for (int j = 1; j < i; j++) {
+ res[i][j] = (res[i - 1][j - 1] + res[i - 1][j]) % MOD;
+ }
+ }
+ return res;
+ }
+
+ private static int[] precomputePop(int max) {
+ int[] res = new int[max];
+ for (int i = 1; i < max; i++) {
+ res[i] = res[i >> 1] + (i & 1);
+ }
+ return res;
+ }
+}
diff --git a/src/main/java/g3501_3600/s3539_find_sum_of_array_product_of_magical_sequences/readme.md b/src/main/java/g3501_3600/s3539_find_sum_of_array_product_of_magical_sequences/readme.md
new file mode 100644
index 000000000..47499759b
--- /dev/null
+++ b/src/main/java/g3501_3600/s3539_find_sum_of_array_product_of_magical_sequences/readme.md
@@ -0,0 +1,55 @@
+3539\. Find Sum of Array Product of Magical Sequences
+
+Hard
+
+You are given two integers, `m` and `k`, and an integer array `nums`.
+
+A sequence of integers `seq` is called **magical** if:
+
+* `seq` has a size of `m`.
+* `0 <= seq[i] < nums.length`
+* The **binary representation** of 2seq[0] + 2seq[1] + ... + 2seq[m - 1] has `k` **set bits**.
+
+The **array product** of this sequence is defined as `prod(seq) = (nums[seq[0]] * nums[seq[1]] * ... * nums[seq[m - 1]])`.
+
+Return the **sum** of the **array products** for all valid **magical** sequences.
+
+Since the answer may be large, return it **modulo** 109 + 7.
+
+A **set bit** refers to a bit in the binary representation of a number that has a value of 1.
+
+**Example 1:**
+
+**Input:** m = 5, k = 5, nums = [1,10,100,10000,1000000]
+
+**Output:** 991600007
+
+**Explanation:**
+
+All permutations of `[0, 1, 2, 3, 4]` are magical sequences, each with an array product of 1013.
+
+**Example 2:**
+
+**Input:** m = 2, k = 2, nums = [5,4,3,2,1]
+
+**Output:** 170
+
+**Explanation:**
+
+The magical sequences are `[0, 1]`, `[0, 2]`, `[0, 3]`, `[0, 4]`, `[1, 0]`, `[1, 2]`, `[1, 3]`, `[1, 4]`, `[2, 0]`, `[2, 1]`, `[2, 3]`, `[2, 4]`, `[3, 0]`, `[3, 1]`, `[3, 2]`, `[3, 4]`, `[4, 0]`, `[4, 1]`, `[4, 2]`, and `[4, 3]`.
+
+**Example 3:**
+
+**Input:** m = 1, k = 1, nums = [28]
+
+**Output:** 28
+
+**Explanation:**
+
+The only magical sequence is `[0]`.
+
+**Constraints:**
+
+* `1 <= k <= m <= 30`
+* `1 <= nums.length <= 50`
+* 1 <= nums[i] <= 108
\ No newline at end of file
diff --git a/src/test/java/g1101_1200/s1195_fizz_buzz_multithreaded/FizzBuzzTest.java b/src/test/java/g1101_1200/s1195_fizz_buzz_multithreaded/FizzBuzzTest.java
index fc69dbb9c..074251030 100644
--- a/src/test/java/g1101_1200/s1195_fizz_buzz_multithreaded/FizzBuzzTest.java
+++ b/src/test/java/g1101_1200/s1195_fizz_buzz_multithreaded/FizzBuzzTest.java
@@ -44,7 +44,7 @@ void fizzBuzz() throws InterruptedException {
}
})
.start();
- TimeUnit.MILLISECONDS.sleep(2000);
+ TimeUnit.MILLISECONDS.sleep(2100);
assertThat(fizz[0] > 0, equalTo(true));
}
diff --git a/src/test/java/g3501_3600/s3536_maximum_product_of_two_digits/SolutionTest.java b/src/test/java/g3501_3600/s3536_maximum_product_of_two_digits/SolutionTest.java
new file mode 100644
index 000000000..09e839783
--- /dev/null
+++ b/src/test/java/g3501_3600/s3536_maximum_product_of_two_digits/SolutionTest.java
@@ -0,0 +1,38 @@
+package g3501_3600.s3536_maximum_product_of_two_digits;
+
+import static org.hamcrest.CoreMatchers.equalTo;
+import static org.hamcrest.MatcherAssert.assertThat;
+
+import org.junit.jupiter.api.Test;
+
+class SolutionTest {
+ @Test
+ void maxProduct() {
+ assertThat(new Solution().maxProduct(31), equalTo(3));
+ }
+
+ @Test
+ void maxProduct2() {
+ assertThat(new Solution().maxProduct(22), equalTo(4));
+ }
+
+ @Test
+ void maxProduct3() {
+ assertThat(new Solution().maxProduct(124), equalTo(8));
+ }
+
+ @Test
+ void maxProduct4() {
+ assertThat(new Solution().maxProduct(453), equalTo(20));
+ }
+
+ @Test
+ void maxProduct5() {
+ assertThat(new Solution().maxProduct(437), equalTo(28));
+ }
+
+ @Test
+ void maxProduct6() {
+ assertThat(new Solution().maxProduct(724), equalTo(28));
+ }
+}
diff --git a/src/test/java/g3501_3600/s3537_fill_a_special_grid/SolutionTest.java b/src/test/java/g3501_3600/s3537_fill_a_special_grid/SolutionTest.java
new file mode 100644
index 000000000..55b7912de
--- /dev/null
+++ b/src/test/java/g3501_3600/s3537_fill_a_special_grid/SolutionTest.java
@@ -0,0 +1,28 @@
+package g3501_3600.s3537_fill_a_special_grid;
+
+import static org.hamcrest.CoreMatchers.equalTo;
+import static org.hamcrest.MatcherAssert.assertThat;
+
+import org.junit.jupiter.api.Test;
+
+class SolutionTest {
+ @Test
+ void specialGrid() {
+ assertThat(new Solution().specialGrid(0), equalTo(new int[][] {{0}}));
+ }
+
+ @Test
+ void specialGrid2() {
+ assertThat(new Solution().specialGrid(1), equalTo(new int[][] {{3, 0}, {2, 1}}));
+ }
+
+ @Test
+ void specialGrid3() {
+ assertThat(
+ new Solution().specialGrid(2),
+ equalTo(
+ new int[][] {
+ {15, 12, 3, 0}, {14, 13, 2, 1}, {11, 8, 7, 4}, {10, 9, 6, 5}
+ }));
+ }
+}
diff --git a/src/test/java/g3501_3600/s3538_merge_operations_for_minimum_travel_time/SolutionTest.java b/src/test/java/g3501_3600/s3538_merge_operations_for_minimum_travel_time/SolutionTest.java
new file mode 100644
index 000000000..1b706647b
--- /dev/null
+++ b/src/test/java/g3501_3600/s3538_merge_operations_for_minimum_travel_time/SolutionTest.java
@@ -0,0 +1,25 @@
+package g3501_3600.s3538_merge_operations_for_minimum_travel_time;
+
+import static org.hamcrest.CoreMatchers.equalTo;
+import static org.hamcrest.MatcherAssert.assertThat;
+
+import org.junit.jupiter.api.Test;
+
+class SolutionTest {
+ @Test
+ void minTravelTime() {
+ assertThat(
+ new Solution()
+ .minTravelTime(10, 4, 1, new int[] {0, 3, 8, 10}, new int[] {5, 8, 3, 6}),
+ equalTo(62));
+ }
+
+ @Test
+ void minTravelTime2() {
+ assertThat(
+ new Solution()
+ .minTravelTime(
+ 5, 5, 1, new int[] {0, 1, 2, 3, 5}, new int[] {8, 3, 9, 3, 3}),
+ equalTo(34));
+ }
+}
diff --git a/src/test/java/g3501_3600/s3539_find_sum_of_array_product_of_magical_sequences/SolutionTest.java b/src/test/java/g3501_3600/s3539_find_sum_of_array_product_of_magical_sequences/SolutionTest.java
new file mode 100644
index 000000000..baeb2bcab
--- /dev/null
+++ b/src/test/java/g3501_3600/s3539_find_sum_of_array_product_of_magical_sequences/SolutionTest.java
@@ -0,0 +1,25 @@
+package g3501_3600.s3539_find_sum_of_array_product_of_magical_sequences;
+
+import static org.hamcrest.CoreMatchers.equalTo;
+import static org.hamcrest.MatcherAssert.assertThat;
+
+import org.junit.jupiter.api.Test;
+
+class SolutionTest {
+ @Test
+ void magicalSum() {
+ assertThat(
+ new Solution().magicalSum(5, 5, new int[] {1, 10, 100, 10000, 1000000}),
+ equalTo(991600007));
+ }
+
+ @Test
+ void magicalSum2() {
+ assertThat(new Solution().magicalSum(2, 2, new int[] {5, 4, 3, 2, 1}), equalTo(170));
+ }
+
+ @Test
+ void magicalSum3() {
+ assertThat(new Solution().magicalSum(1, 1, new int[] {28}), equalTo(28));
+ }
+}